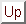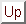
Equation (
) may also be used for
a simple order-of-magnitude estimate of the effect on seeing caused by
the temperature fluctuations caused by free convection from a warmer
dome floor.
Consider the geometry of fig. .
If the dome diameter is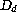 
,
the mean height
of the air volume crossed by the optical beam with respect to the heat
exchange surface will be about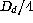 
. Assuming for the constant b the value of 2.68
determined for the
atmospheric surface layer (see equation ()) and taking
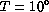C, we find:
Considering that the light beam travels three times between the
primary and the secondary mirror
, the total light path inside the protected volume
of the
dome will be 
and from
equation
(), a rough estimate of
the dome seeing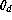 
will be
given by
q_s is the normalized surface heat flux (i.e. divided by air density and specific heat, typically a factor 1000) with dimentions [K.m/s].
Equation (5.29) is plotted in fig. for two
typical
values of enclosure size: free convection flow in the enclosure volume
will begin to cause significant seeing effects (
0.4 arcsec) in the light beam with a
heat flux of the order of 20 W/m
. Considering that a
typical free convection heat transfer rate would be 3 W/m
K at
the floor, one should then expect a seeing contribution of about 0.06
to 0.08 arcsec per deg K of floor-air temperature difference.
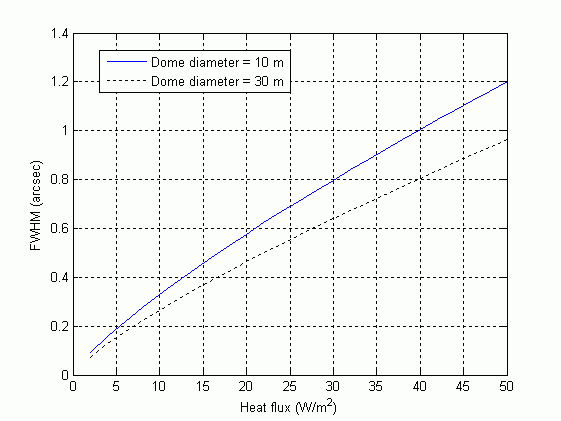
Figure: Order-of-magnitude
value of seeing FWHM caused by a warmer dome floor.
Relationship of the same quantitative order between heat flux,
distance from the exchange
surface and seeing are likely applicable also to
other potential sources of free convection located inside the enclosure
(e.g. items G and I in fig. ).
However, in view of the smaller exchange surface areas of walls and
other heat dissipating objects with respect to the inner air volume,
the seeing rate per deg K of surface-air temperature difference
will be quite lower than for the floor.
The rate of dome seeing per floor-air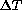 
of 0.06 to 0.08 arcsec/K which is estimated here
indeed explains the high seeing values
experienced during the first years of operation by many
telescopes of 4-m class built in the 70s, like the ESO 3.6-m
and the CFHT. These telescopes are enclosed in large concrete/steel
buildings with no natural ventilation and,
as the inner dome thermal environment was hardly or poorly controlled,
the different heat capacities of the concrete base, the primary mirror,
the
telescope structure and the dome inevitably caused large differences of
temperatures. Measurements at the ESO 3.6-m telescope performed by the
author [Zago 84] and [Schmider] before the installation of
an improved thermal control
system in the dome,
show that the temperature difference between the dome floor
and the interior air is frequently of the order of 5 K and raise at
times up to 10 K.
As we have already mentioned in section above,
the thermal control of most of these domes has been improved in the
meantime, so that surface-air 
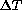now hardly exceed 1 or 2 K in the worst cases. Newer
telescopes such as the MMT and the NTT have been built inside lighter
enclosures which also allow natural ventilation. As a consequence,
dome seeing, in the proper meaning of seeing created by
large convection flow patterns in
the dome enclosure,
is no more a critical factor of telescope performance nowadays.
Therefore there is not much opportunity nor perhaps
interest to investigate in detail a
matter which appears pragmatically solved.
