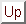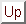
A general characterization of free convection at a surface of characteristic length L is given by the following dimensionless numbers which are derived from the governing equations (see for instance [Incoprera], p. 493):
is affected by free convection generated
by temperature differences between air and the floor of the dome.
The floor-air temperature difference will generate a system of
convection cells by which the heat is carried in the dome inner air
volume.
Since the flow conditions around a telescope are generally
too complex to allow
a rigorous modelisation of theair volumes affected by the seeing
effect, it will be of interest to understand the similarity
that rules the effect
of changes of one or more parameters on the seeing,
thereby deriving the criteria for interpreting the data obtained from
mirrors and telescopes of different scales and conditions.
In an extreme simplification we will consider the height from the
floor as the only geometrical parameter.
Mean statistical values of turbulent quantities
may then be obtained through similarity
theory (see section ). Following [Wyngaard],
we take as scaling variables
of the free convection field from a plane horizontal surface
the quantities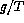 
, q
and z. Dimensional
reasoning leads then to
where b is a constant. Rearranging gives:
which, within the constant factor, is equation ()
which had been derived for the unstable limit conditions
of a turbulent boundary flow.
Equation () is a convenient expression to derive
a relationship of the integrated seeing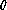 
with the flow scaling variables.
Noting that g and T, as well as air density and specific
heat are not scalable, and assuming further that the height dependency
will be constant through all scales, the scales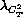 
and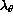 
of seeing
are related to the scale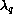 
of surface flux (the normalized
heat transfer rate) as
and, recalling equation (),
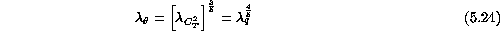
Noting that q is a likely function of temperature difference and upward flow speed, dimensional analysis gives:
From the Froude number criterion, we have:
Thus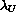 
is approximately:
One gets:
and finally
