Mirror seeing is caused by natural or weakly mixed convection over a mirror warmer than ambient air. The seeing effect is generated in a thin region just above the viscous-conductive layer where the temperature fluctuations are largest and most intermittent. If its cause could be visualized, seeing would appear to come from a thin but very turbulent layer "floating" a few millimeters above the surface.
The results of several experiments performed by various researchers[2] [3] [10] , have been processed to get a homogeneous database[10] . In still air, mirror seeing appears not to depend on the mirror size. For the purpose of engineering parametric studies the following relationship is proposed:
with a possible spread of 25%. This relationship is validated in particular by the author's analysis of the log files of all observations performed during the years 1991, 1992 and 1993 at the CFHT, where it is shown that mirror seeing is indeed the only remaining cause of observatory-made seeing[10].
The effect of mirror inclination is more controversial: it is reported to be large for a small 25-cm mirror[3] but does not appear in our analysis of the 3.6-m CFHT observations data.
The author[10] formulates the hypothesis
that the average amplitude of the seeing would be essentially a function
of the surface heat flux. The profile of ![]() can then be described by a similarity equation (19),
valid down to the interface with the tiny viscous-conductive layer.
can then be described by a similarity equation (19),
valid down to the interface with the tiny viscous-conductive layer.
The maximum value of ![]() will be found at the top of the viscous conductive layer, the thickness
of which is computed by the expression from [5]
as:
will be found at the top of the viscous conductive layer, the thickness
of which is computed by the expression from [5]
as:
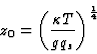
![]() is zero at the surface and will be linearly interpolated in the viscous
conductive layer. Thus the vertical profile of
is zero at the surface and will be linearly interpolated in the viscous
conductive layer. Thus the vertical profile of ![]() is described by
is described by
| = | 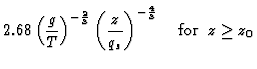 |
(19) | |
| = | (20) |
![\begin{displaymath}\theta = 5.182\cdot 10^{-5} \, \lambda^{-1/5}\left( 80 \cdo......ght)^{3/5}\left[ \int_{\rm H}{C_T^{2}(z)} dz\right]^{3/5}\end{displaymath}](img54.gif) |
(21) |
| [IMAGE
]
Figure 6: Mirror seeing for an horizontal mirror in free convection for Tm > Ta. Laboratory data experiments 2, 3, 10 performed in various ranges of temperatures are compared with expression (18) and with the similarity model (19). |
Next:Mirror seeing in forced Up:DOME SEEING Previous:Seeing caused by heat
Lorenzo Zago