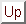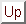
Discussion of experimental data
We have seen that mirror seeing due to pure free convection
should be proportional to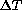 
with an exponent of 1.2.
Examination of the experimental
measurements leads to the following conclusions:
indicate a proportionality
factor of 0.38 arcsec/K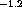
.
lies between 0.25 and 0.34, although in fact the data would be better
fitted with an exponent greater than 1.2.
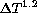lies between 0.28 (for 
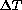= 8K) and 0.45
(for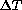 
= 2K). The exponent would appear here to be lower than
1.
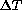s up to 22K factors between 0.25 and 0.54.
The discrepancies between the various experiments must not surprise as the measurement methods, the experiment set-ups, the range of temperatures explored and the environmental conditions differed greatly. Nevertheless the basic concordance of data over the large range of mirror diameters and other conditions provides some useful indications:
) it
appears that mirror seeing is
a quite "robust" phenomenon as its quantification does not depend
exceedingly on the particular conditions of the flow regime.
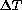s, associated with very low
Raleigh numbers, it must be concluded that also fluctuations and
instabilities in
laminar flow regimes do produce seeing whose magnitude is of the
same order as in fully turbulent regimes.
Emphasizing the weight to the CFHT data, we will here propose the following relationship for the purpose of engineering parametric studies:
One should make allowance for possible variations of the order to
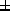25%.
Fig. shows the reasonable agreement of
equation () with respect to all the laboratory data.
\
[IMAGE ]
Figure: Mirror seeing for an horizontal mirror in free
convection
for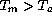 
. Laboratory data from experiments performed in
various ranges of temperatures are compared with expression
(5.44) and
with the similarity profile model of equations (5.45-46).
Similarity theory model
In section we have illustrated how the
production of mirror seeing takes place very close to the
surface, in the region near the interface between the
viscous conductive layer and the emerging plumes of warmer air.
It follows that the phenomenon depends essentially only on one, namely
vertical, geometrical coordinate.
The hypothesis was expressed
that the profile of the temperature structure coefficient
above the viscous conductive layer
over a mirror should follow the same similarity law
() as in the
atmospheric surface layer, in spite of the large difference of
geometric scale.
The maximum value of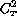 
will be found at the top of
the viscous conductive layer, the thickness of which is computed by
the expression from [Townsend] as:
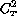is zero at the surface and will be linearly interpolated in
the viscous conductive layer.
Thus the vertical profile of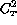 
is described by
The seeing FWHM angle is then obtained by integrating equation
() twice
over the height significant for seeing effects:
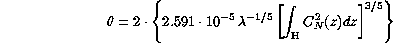
where 
is given by equation ():
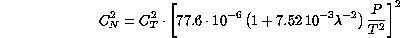
obtaining:
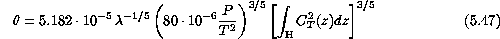
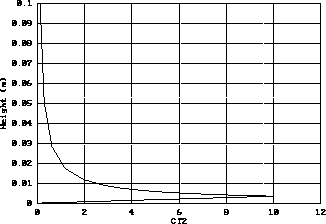
Figure: Example of computed profile
of the temperature structure coefficient 
(mirror diameter 62-cm,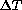 
= 1K, sea
level conditions). The integrated FWHM is 0.4 arcsec.
This model has been used to simulate all the laboratory
experiments described above. In these simulations, the surface flux
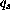was computed
by the textbook
relationship between the Nusselt and Raleigh numbers
for the laminar regime (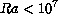
):
A computed profile of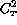 
is shown in
fig. . One may note that in this typical example
(mirror diameter 62-cm, mirror-air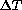 
= 1K) the near totality
of mirror seeing is produced in the first 2 cm above the mirror
surface.
The integral seeing values resulting
from the simulations are plotted in fig. over the
experimental data.
The good agreement indicates that a similarity
model described by equations (5.45-46) does account well for
the observed seeing effects.
![[IMAGE ]](img726.gif){kind=link}