


Next: FOCam data
Up: Analysis of telescope
Previous: Analysis procedure
After the preliminary screening 1662 observation records were
retained.
The general statistics of the FWHM measurements is
Average: 0.65 arcsec
Median: 0.61 arcsec
Rms: 0.18 arcsec
Minimum: 0.35 arcsec
One should note here that the median values are more significant
of general performance than arithmetic averages.
Image quality and seeing
statistics follow an approximately log-normal distribution
(see fig.  ) in which the average is significantly
larger than the median. Therefore plain regression
techniques, which assume a Gaussian distribution, cannot be
applied directly on distributions of FWHM values and we will here use
the method of collapsing the data to median values binned over small
intervals of a dependent variable before applying fitting techniques.
) in which the average is significantly
larger than the median. Therefore plain regression
techniques, which assume a Gaussian distribution, cannot be
applied directly on distributions of FWHM values and we will here use
the method of collapsing the data to median values binned over small
intervals of a dependent variable before applying fitting techniques.
Figure: Histogram of FWHM data
from HRCam: note the typical log-normal distribution.
A first verification establishes that the HRCam FWHM distribution does not
appear to show a significant dependency on wind speed:
Median for U < 5 m/s: 0.61 arcsec
Median for 5 < U < 10 m/s: 0.64 arcsec
Median for 10 < U < 15 m/s: 0.64 arcsec
Median for U > 15 m/s: 0.58 arcsec
The temperature data measured at several locations around the
telescope and in the dome (see table  ) confirm
that the CFHT dome environment is almost permanently characterized
by a stable thermal stratification. In the vast majority of
the observations the air temperature above the
primary mirror is lower than the one near the top ring,
which in turn is lower than the external air temperature - see
fig.
) confirm
that the CFHT dome environment is almost permanently characterized
by a stable thermal stratification. In the vast majority of
the observations the air temperature above the
primary mirror is lower than the one near the top ring,
which in turn is lower than the external air temperature - see
fig.  .
This stratification effectively "damps"
free convection flow patterns and any related turbulence.
Indeed one does not find any
seeing that could be attributed to
.
This stratification effectively "damps"
free convection flow patterns and any related turbulence.
Indeed one does not find any
seeing that could be attributed to 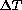 's between air and floor
and dome surfaces.
's between air and floor
and dome surfaces.
The temperature of the primary mirror stays generally very close to
the one of air just above it: the average of the mirror surface-air
temperature difference 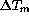 is + 0.05K, with a rms
of 0.47K. As shown by fig.
is + 0.05K, with a rms
of 0.47K. As shown by fig.  ,
, 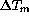 and
and 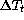 are
visibly correlated (the correlation coefficient is 0.75)
while this hardly appears to be the case of the pairs consisting of
are
visibly correlated (the correlation coefficient is 0.75)
while this hardly appears to be the case of the pairs consisting of
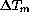 and
and 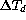 , although the correlation coefficient is
nevertheless 0.14 .
, although the correlation coefficient is
nevertheless 0.14 .
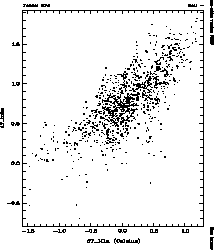
Figure: Scatter plot of 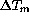 versus
versus 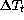
Fig.  shows a scatter plot of FWHM values with respect to
shows a scatter plot of FWHM values with respect to
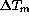 . In order to avoid bias from the airmass effect
only observations with
. In order to avoid bias from the airmass effect
only observations with 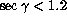 are taken (984 records).
Binned medians are also shown.
are taken (984 records).
Binned medians are also shown.
For 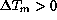 a trend to larger median FWHM is noticeable.
a trend to larger median FWHM is noticeable.
For 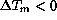 no influence is noted, if one excepts a group of
values for which
no influence is noted, if one excepts a group of
values for which 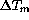 is less than -1K,
which belong all to a same observation
sequence. Therefore the higher average seeing of this sequence
may well be due to increased natural seeing accidentally occurring at
the time.
is less than -1K,
which belong all to a same observation
sequence. Therefore the higher average seeing of this sequence
may well be due to increased natural seeing accidentally occurring at
the time.
[IMAGE ]
Figure: Scatter plot of HRCam
FWHM versus the temperature difference
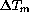 between the mirror surface and the surrounding air.
Binned median values and the are also shown.
between the mirror surface and the surrounding air.
Binned median values and the are also shown.
Fig.  shows a scatter plot of FWHM values with respect to
the temperature difference
shows a scatter plot of FWHM values with respect to
the temperature difference 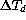 between the dome interior and the
outside air.
Again only observations with
between the dome interior and the
outside air.
Again only observations with 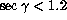 are considered.
Note that because of the dome floor cooling system,
the dome interior is amost always colder than the outside air.
are considered.
Note that because of the dome floor cooling system,
the dome interior is amost always colder than the outside air.
For 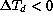 no dependency is appearing.
no dependency is appearing.
For 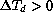 there may seem to be a trend toward increased
seeing, but too few data points exist to derive any
significant conclusion.
there may seem to be a trend toward increased
seeing, but too few data points exist to derive any
significant conclusion.
[IMAGE ]
Figure: Scatter plot of HRCam FWHM versus
the dome-outside temperature difference 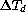 .
.
In order to find correlation coefficients that would fit equations
( ) and (
) and ( ), it is necessary to get first an
estimate of the fixed telescope/instrument error
), it is necessary to get first an
estimate of the fixed telescope/instrument error  .
By correlating with respect to
.
By correlating with respect to 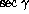 a subset of FWHM values for which the temperature dependent
effects are absent, one can estimate the mean natural seeing and
the fixed error due to the instrument. This subset, which includes only
FWHM values
corresponding to
a subset of FWHM values for which the temperature dependent
effects are absent, one can estimate the mean natural seeing and
the fixed error due to the instrument. This subset, which includes only
FWHM values
corresponding to 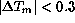 K and
K and 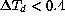 K (858
records), is plotted in fig.
K (858
records), is plotted in fig.  .
Noting that, when
.
Noting that, when 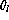 and
and  are nil,
equation (
are nil,
equation ( ) becomes
) becomes

a least square fit on the binned median values of the selected subset
gives a fixed error due to the instrument
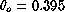 arcsec
arcsec
while the median natural seeing is evaluated as
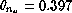 arcsec
arcsec
[IMAGE ]
Figure: HRCam FWHM versus  in absence of mirror and
dome seeing
in absence of mirror and
dome seeing
To find a parameterization for the FWHM versus 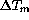 relationship,
we consider a subset with
relationship,
we consider a subset with 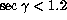 (fig.
(fig.  ).
Noting that
).
Noting that 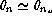 in this case,
equation (
in this case,
equation ( ), combined with (
), combined with ( ) gives
) gives
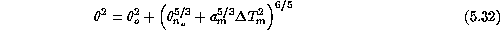
For 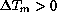 , a least square fit gives
, a least square fit gives 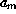 = 0.38
which results in the following parameterization for the mirror seeing
contribution:
= 0.38
which results in the following parameterization for the mirror seeing
contribution:
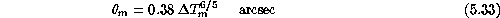
This fit is also plotted on fig.  .
.
For 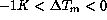 the slope is practically nil, while for
the slope is practically nil, while for
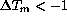 K, the data are inconclusive, as explained above.
K, the data are inconclusive, as explained above.
So far then, recalling that no dependency appears with respect to
the temperature difference 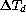 between the dome interior and the
outside air,
the HRCam performance appears represented by the following
relationship:
between the dome interior and the
outside air,
the HRCam performance appears represented by the following
relationship:
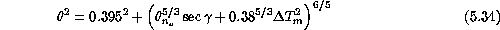
Other possible dependencies were sought by analyzing the values
of natural seeing extracted by means of equation ( )
)
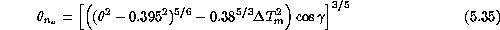
versus other temperature differences
obtainable from the sensors listed in table  .
None could be determined.
For instance, fig.
.
None could be determined.
For instance, fig.  shows a plot of
shows a plot of 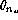 values
computed from (
values
computed from ( ) with respect to the temperature gradient
along the tube
) with respect to the temperature gradient
along the tube 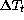 : no correlation is apparent.
: no correlation is apparent.
Noting that we had not taken into account the mirror orientation
in the parameterization for mirror seeing ( ),
we have analyzed also
a subset of
),
we have analyzed also
a subset of 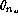 values in which
values in which 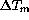 is > 0.5K
with respect to
is > 0.5K
with respect to 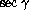 - fig.
- fig. . Also
in this case no correlation is apparent.
. Also
in this case no correlation is apparent.
Finally, the median of 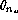 over the entire data set (1662 records)
is 0.39 arcsec, very close to the value of 0.397 arcsec evaluated
previously.
over the entire data set (1662 records)
is 0.39 arcsec, very close to the value of 0.397 arcsec evaluated
previously.
Equation ( ) can thus be considered as
verified for the HRCam observations.
) can thus be considered as
verified for the HRCam observations.
[IMAGE ]
Figure: HRCam computed natural seeing 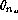 with respect to the temperature gradient along the tube
with respect to the temperature gradient along the tube 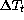 .
.
[IMAGE ]
Figure: Check for unaccounted effects of telescope orientation
on mirror seeing:
HRCam computed natural seeing 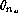 with respect to
with respect to  (only data with
(only data with  0.5K)
0.5K)



Next: FOCam data
Up: Analysis of telescope
Previous: Analysis procedure
Lorenzo Zago, lorenzo.zago@heig-vd.ch,
Mon Nov 6 23:33:14 GMT+0100 1995
 ) in which the average is significantly
larger than the median. Therefore plain regression
techniques, which assume a Gaussian distribution, cannot be
applied directly on distributions of FWHM values and we will here use
the method of collapsing the data to median values binned over small
intervals of a dependent variable before applying fitting techniques.
) in which the average is significantly
larger than the median. Therefore plain regression
techniques, which assume a Gaussian distribution, cannot be
applied directly on distributions of FWHM values and we will here use
the method of collapsing the data to median values binned over small
intervals of a dependent variable before applying fitting techniques.




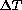 's between air and floor
and dome surfaces.
's between air and floor
and dome surfaces.
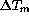 is + 0.05K, with a rms
of 0.47K. As shown by fig.
is + 0.05K, with a rms
of 0.47K. As shown by fig. 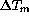 and
and 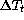 are
visibly correlated (the correlation coefficient is 0.75)
while this hardly appears to be the case of the pairs consisting of
are
visibly correlated (the correlation coefficient is 0.75)
while this hardly appears to be the case of the pairs consisting of
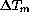 and
and 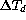 , although the correlation coefficient is
nevertheless 0.14 .
, although the correlation coefficient is
nevertheless 0.14 .

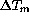 versus
versus 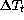
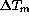 . In order to avoid bias from the airmass effect
only observations with
. In order to avoid bias from the airmass effect
only observations with 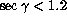 are taken (984 records).
Binned medians are also shown.
are taken (984 records).
Binned medians are also shown. 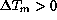 a trend to larger median FWHM is noticeable.
a trend to larger median FWHM is noticeable.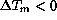 no influence is noted, if one excepts a group of
values for which
no influence is noted, if one excepts a group of
values for which 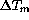 is less than -1K,
which belong all to a same observation
sequence. Therefore the higher average seeing of this sequence
may well be due to increased natural seeing accidentally occurring at
the time.
is less than -1K,
which belong all to a same observation
sequence. Therefore the higher average seeing of this sequence
may well be due to increased natural seeing accidentally occurring at
the time.
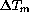 between the mirror surface and the surrounding air.
Binned median values and the are also shown.
between the mirror surface and the surrounding air.
Binned median values and the are also shown.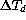 between the dome interior and the
outside air.
Again only observations with
between the dome interior and the
outside air.
Again only observations with 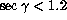 are considered.
Note that because of the dome floor cooling system,
the dome interior is amost always colder than the outside air.
are considered.
Note that because of the dome floor cooling system,
the dome interior is amost always colder than the outside air. 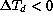 no dependency is appearing.
no dependency is appearing. 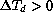 there may seem to be a trend toward increased
seeing, but too few data points exist to derive any
significant conclusion.
there may seem to be a trend toward increased
seeing, but too few data points exist to derive any
significant conclusion.
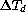 .
. 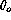 .
By correlating with respect to
.
By correlating with respect to 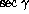 a subset of FWHM values for which the temperature dependent
effects are absent, one can estimate the mean natural seeing and
the fixed error due to the instrument. This subset, which includes only
FWHM values
corresponding to
a subset of FWHM values for which the temperature dependent
effects are absent, one can estimate the mean natural seeing and
the fixed error due to the instrument. This subset, which includes only
FWHM values
corresponding to 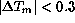 K and
K and 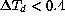 K (858
records), is plotted in fig.
K (858
records), is plotted in fig. 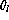 and
and 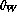 are nil,
equation (
are nil,
equation (
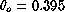 arcsec
arcsec
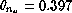 arcsec
arcsec
 in absence of mirror and
dome seeing
in absence of mirror and
dome seeing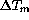 relationship,
we consider a subset with
relationship,
we consider a subset with 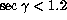 (fig.
(fig. 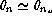 in this case,
equation (
in this case,
equation (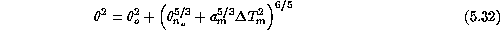
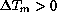 , a least square fit gives
, a least square fit gives 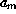 = 0.38
which results in the following parameterization for the mirror seeing
contribution:
= 0.38
which results in the following parameterization for the mirror seeing
contribution: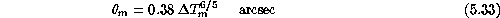
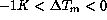 the slope is practically nil, while for
the slope is practically nil, while for
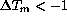 K, the data are inconclusive, as explained above.
K, the data are inconclusive, as explained above.
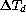 between the dome interior and the
outside air,
the HRCam performance appears represented by the following
relationship:
between the dome interior and the
outside air,
the HRCam performance appears represented by the following
relationship:
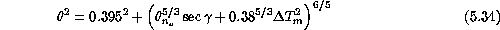
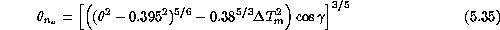
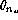 values
computed from (
values
computed from (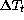 : no correlation is apparent.
: no correlation is apparent.
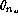 values in which
values in which 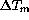 is > 0.5K
with respect to
is > 0.5K
with respect to 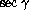 - fig.
- fig.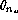 over the entire data set (1662 records)
is 0.39 arcsec, very close to the value of 0.397 arcsec evaluated
previously.
over the entire data set (1662 records)
is 0.39 arcsec, very close to the value of 0.397 arcsec evaluated
previously. 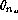 with respect to the temperature gradient along the tube
with respect to the temperature gradient along the tube 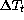 .
.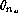 with respect to
with respect to 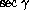 (only data with
(only data with 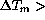 0.5K)
0.5K)