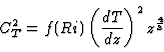 |
(10) |
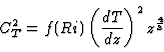 |
(10) |
where Ri is the Richardson number:
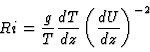
The function f(Ri) (tabulated by Wyngaard[9]) is obtained from experimental measurements.
By choosing other scaling variables, namely the friction velocity u* and the normalized surface heat flux q (in K m s-1), and as the stability parameter the ratio z/L, where L is the Monin-Obukhov length
Wyngaard[9] obtains another expression
for ![]() :
:
 |
(11) |
where g(z/L) is an empirical function evaluated from experimental data as:
| g(z/L) | = | 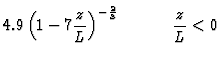 |
(12) |
| g(z/L) | = | 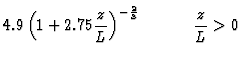 |
(13) |
We note also that ![]() can also be put in relation with the outer scale of turbulence Lu:
can also be put in relation with the outer scale of turbulence Lu:
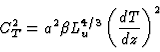 |
(14) |
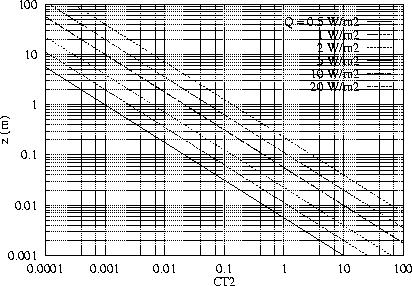 |