



Next: Full Width Half Maximum
Up: SEEING
Previous: SEEING
In analogy with the theory of the turbulent velocity field,
Tatarskii[6] finds an inertial domain, between
the outer scale of turbulence L and l
where the temperature turbulent variations are defined by a
statistical structure function
has the form:
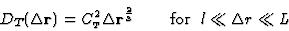 |
(2) |
where
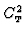 is the temperature structure coefficient.
is the temperature structure coefficient.
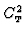 characterizes completely the local thermal turbulence at
a give time, has SI units (K2 m-2/3) and is therefore formally
defined as:
characterizes completely the local thermal turbulence at
a give time, has SI units (K2 m-2/3) and is therefore formally
defined as:
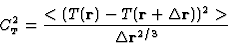 |
(3) |
for a separation
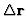 in the inertial domain.
in the inertial domain.
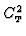 is also related to the one-dimensional
temperature spectrum which in the inertial domain has the form:
is also related to the one-dimensional
temperature spectrum which in the inertial domain has the form:
 |
(4) |
where 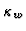 is the streamwise component of wavenumber.
is the streamwise component of wavenumber.
Moreover, Tatarskii[6] notes that in the inertial domain
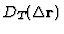 should be a function of only
the dissipation rate of kinetic energy
should be a function of only
the dissipation rate of kinetic energy 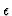 ,
,
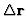 and the temperature dissipation rate
and the temperature dissipation rate
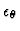 .
Dimensional reasoning leads then to
.
Dimensional reasoning leads then to
 |
(5) |
where a2 is a constant found to be equal to about 3.
Analog statistical properties may be applied to
the index of refraction and one may define a
structure coefficient of the index of refraction
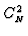 .
From equation (1) and ignoring the very minor
effect of humidity,
.
From equation (1) and ignoring the very minor
effect of humidity,
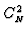 is related to
is related to
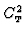 by:
by:
![\begin{displaymath}
C_{\scriptscriptstyle N}^2 =
C_{\scriptscriptstyle T}^2 \...
....52\,10^{-3}\lambda^{-2} \right)
\frac{P}{T^{2}}\right]^{2}
\end{displaymath}](img20.gif) |
(6) |
where 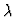 is the wavelength.
is the wavelength.




Next: Full Width Half Maximum
Up: SEEING
Previous: SEEING
Lorenzo Zago
Aug 2010
![]() is also related to the one-dimensional
temperature spectrum which in the inertial domain has the form:
is also related to the one-dimensional
temperature spectrum which in the inertial domain has the form:
![]() .
From equation (1) and ignoring the very minor
effect of humidity,
.
From equation (1) and ignoring the very minor
effect of humidity,
![]() is related to
is related to
![]() by:
by: